R3-[Q-Shape] - Research: Qualitative Spatial Reasoning
Variants of the Dipole Relation Algebra (DRA)
In [MRW00] a qualitative spatial calculus dealing with two directed line segments, in the following also called dipole, as basic entities was presented. It is based on calculus presented by Schlieder in [Sch95]. These dipoles are used for representing spatial objects with intrinsic orientation. A dipole ![]() is defined by two points, the start point
is defined by two points, the start point ![]() and the end point
and the end point ![]() . The presented calculus deals with the orientation of two dipoles. An example of the relation
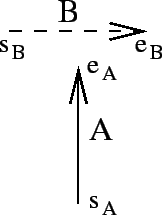
. The presented calculus deals with the orientation of two dipoles. An example of the relation ![]() is shown in the figure below. The four letters denote the relative position (e.g. left or right) of one of the points to the other dipole:
is shown in the figure below. The four letters denote the relative position (e.g. left or right) of one of the points to the other dipole: ![]()
 |
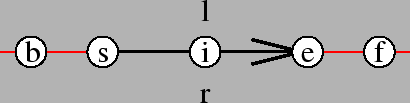
Based on a two dimensional continuous space, ![]() , the location and orientation of two different dipoles can be distinguished by representing the relative position of start and end points. In the original version by Schlieder no three points were allowed on a line resulting in 14 base relations [Sch95]. In [MRW00] this restriction was weakened to allowing distinctions between left or right and the same start or end point if no more than three points are allowed on a line, and without this restriction [DM05] back, interior and front additionally.
, the location and orientation of two different dipoles can be distinguished by representing the relative position of start and end points. In the original version by Schlieder no three points were allowed on a line resulting in 14 base relations [Sch95]. In [MRW00] this restriction was weakened to allowing distinctions between left or right and the same start or end point if no more than three points are allowed on a line, and without this restriction [DM05] back, interior and front additionally.
 |
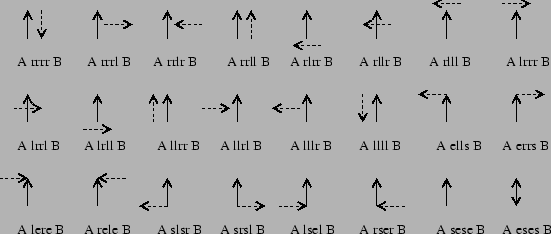
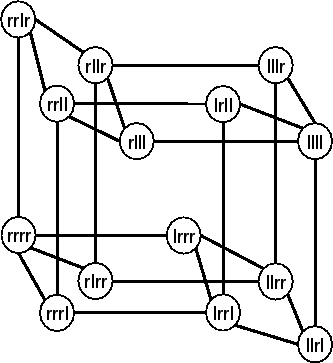
The view of [MRW00] leads to 24 jointly exhaustive and pairwise disjoint (jepd) basic relations, i.e. between any two dipoles exactly one relation holds at any time. Additionally they build up a relation algebra with 24 basic relations. These relations build up a quite coarse distinction between different orientations, thus we will call this algebra ![]() . A visualization is shown in the figure underneath. In contrast the calculus of Schlieder [Sch95] does not build up a relation algebra. Because of forming a relation algebra standard constraint-based reasoning techniques can be applied. The unrestricted version leads to a relation algebra with 72 basic relations. We will call this fine grained algebra
. A visualization is shown in the figure underneath. In contrast the calculus of Schlieder [Sch95] does not build up a relation algebra. Because of forming a relation algebra standard constraint-based reasoning techniques can be applied. The unrestricted version leads to a relation algebra with 72 basic relations. We will call this fine grained algebra ![]() . For a detailed description of the calculus' properties we refer to [MRW00].
. For a detailed description of the calculus' properties we refer to [MRW00].
 |
Extended Dipole Relation Algebra
Unfortunately ![]() may not be sufficient for robot navigation tasks, because even in this finer grained version many different dipole configurations are pooled in one relation. Thus we extend the representation with additional orientation knowledge and derive a more fine grained relation algebra with additional orientation distinctions. We will call this
may not be sufficient for robot navigation tasks, because even in this finer grained version many different dipole configurations are pooled in one relation. Thus we extend the representation with additional orientation knowledge and derive a more fine grained relation algebra with additional orientation distinctions. We will call this ![]() .
.
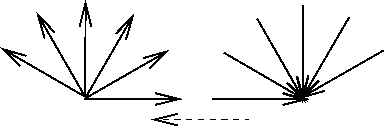 |
In the figure above for example the large configuration space for the rrrr relation is visualized. This might lead to quite squiggly paths if using these concepts for robot navigation. Other relations being extremely coarse are llrr, rrll and llll. We would expect a more goal directed behavior breaking up the relations by regarding the angle spanned by the two dipoles qualitatively. This gives us an important additional distinguishing feature with four distinctive values. These qualitative distinctions are parallelism (![]() ) or anti-parallelism (
) or anti-parallelism (![]() ) and mathematically positive and negative angles between A and B, leading to three refining relations for each of the four above mentioned relations (see figure below). Thus we call this algebra
) and mathematically positive and negative angles between A and B, leading to three refining relations for each of the four above mentioned relations (see figure below). Thus we call this algebra ![]() being an extension of the fine grained relation algebra
being an extension of the fine grained relation algebra ![]() with additional distinctions based on ``parallelism''.
with additional distinctions based on ``parallelism''.
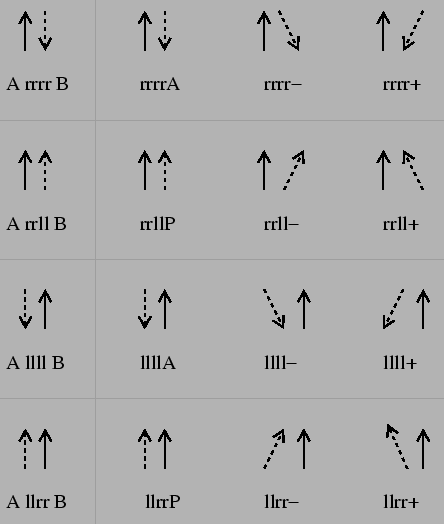 |
For the other relations a '![]() ', '
', '![]() ', '
', '![]() ', or '
', or '![]() ' is already determined by the original base relation. For a complete list of the resulting
' is already determined by the original base relation. For a complete list of the resulting ![]() algebra we refer to [DM05].
algebra we refer to [DM05].
The Conceptual Neighborhood Structure of the Dipole Relation Algebras
The conceptual neighborhood (CNH) structure of a calculus is necessary for solving problems by neighborhood based reasoning. In [Sch95] the neighborhood structure of the 14 base relations of the originating Dipole Calcus was already given.
The CNH-graphs and alternatively CNH-tables of the other calculi
 (iconic table in pdf (360K)) (machine readable in csv) (grid table in pdf)
(iconic table in pdf (360K)) (machine readable in csv) (grid table in pdf) (iconic table in pdf (2.0MB)) (machine readable in csv) (grid table in pdf)
(iconic table in pdf (2.0MB)) (machine readable in csv) (grid table in pdf) (iconic table in pdf (2.0MB)) (machine readable in csv) (grid table in pdf)
(iconic table in pdf (2.0MB)) (machine readable in csv) (grid table in pdf)
Restricting to relations suited for robotic navigational tasks where dipoles represent solid objects (other non solid objects like doorways may also be represented by dipoles) we end up with only 40 base relations, thus giving us a condensed CNH-graphs.
 |
Bibliography
[DM05]: Frank Dylla and Reinhard Moratz. Exploiting Qualitative Spatial Neighborhoods in the Situation Calculus. In Lecture Notes in Artificial Intelligence 3343 - Spatial Cognition IV Reasoning, Action, Interaction, pages 304-322, 2005.
[MRW00]: Reinhard Moratz, Jochen Renz, and Diedrich Wolter. Qualitative spatial reasoning about line segments. In Proceedings of ECAI 2000, pages 234-238, 2000.
[Ren01]: Jochen Renz. A spatial odyssey of the interval algebra: 1. directed intervals. In Proceedings of IJCAI 2001, pages 51-56, 2001.
[Sch95]: C. Schlieder. Reasoning About Ordering. In Spatial Information Theory - A Theoretical Basis for GIS (COSIT'95), pages 341-349, Springer, 1995.




